Teorema geométrico de Euler

En geometría, el teorema de Euler establece que la distancia d entre el circuncentro y el incentro de un triángulo, cumple la relación siguiente:^[1]​^[2]​^[3]​^[4]​

${\displaystyle d^{2}=R(R-2r)\,}$

o de forma equivalente

${\displaystyle {\frac {1}{R-d}} {\frac {1}{R d}}={\frac {1}{r}}}$

donde R y r denotan el circunradio y el inradio (los radios de la circunferencia circunscrita y de la circunferencia inscrita respectivamente).

El teorema recibe su nombre en memoria de Leonhard Euler, quien lo publicó en 1767,^[5]​ aunque el mismo resultado ya había sido dado a conocer por William Chapple en 1746.^[6]​

Del teorema se deduce la Desigualdad de Euler:^[2]​^[3]​

${\displaystyle R\geq 2r,}$

que se convierte en una igualdad solo en el caso del triángulo equilátero.^[7]​^{: p. 198}

Demostración

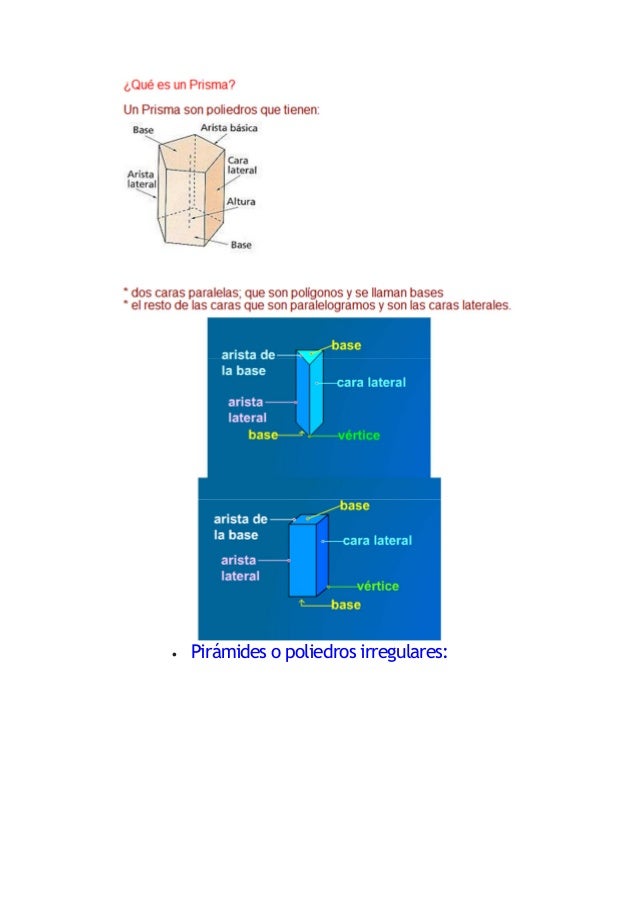
Siendo O el circuncentro de triángulo ABC, e I su incentro, la extensión de AI cruza la circunferencia circunscrita en L. Entonces, L es el punto medio del arco BC. Se unen LO y se extiende hasta cruzar la circunferencia circunscrita en M. Se construye ahora una perpendicular a AB, desde I, siendo D su pie, así que ID = r. No es difícil de probar que el triángulo ADI es similar al triángulo MBL, así que ID / BL = AI / ML; y por lo tanto ID × ML = AI × BL. En consecuencia, 2Rr = AI × BL. Únase BI. Debido a que

∠ BIL = ∠ A / 2 ∠ ABC / 2,

∠ IBL = ∠ ABC / 2 ∠ CBL = ∠ ABC / 2 ∠ A / 2,

se tiene que ∠ BIL = ∠ IBL, y así BL = IL, y AI × IL = 2 Rr. Extendiendo OI de modo que cruce la circunferencia circunscrita en P y Q; entonces PI × QI = AI × IL = 2Rr, así que (R d)(R − d) = 2Rr, entonces d² = R(R - 2r).

Versión fuerte de la desigualdad

Una versión más fuerte es^[7]​^{: p. 198}

${\displaystyle {\frac {R}{r}}\geq {\frac {abc a^{3} b^{3} c^{3}}{2abc}}\geq {\frac {a}{b}} {\frac {b}{c}} {\frac {c}{a}}-1\geq {\frac {2}{3}}\left({\frac {a}{b}} {\frac {b}{c}} {\frac {c}{a}}\right)\geq 2.}$

Véase también

• Teorema de Fuss para la relación entre las mismas tres variables en cuadriláteros bicéntricos.
• Teorema de clausura de Poncelet, mostrando que hay una infinidad de triángulos con el mismo R, r, y d.
• Anexo:Desigualdades del triángulo

Referencias